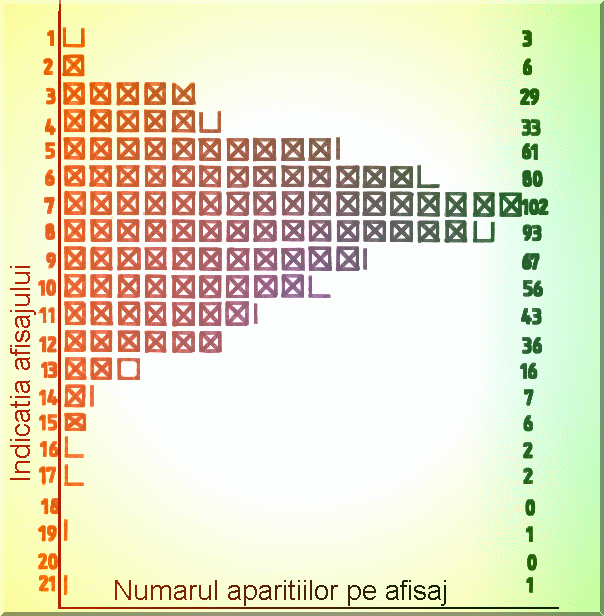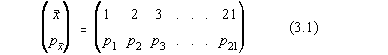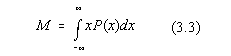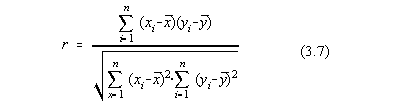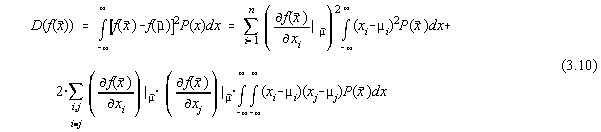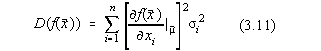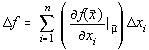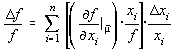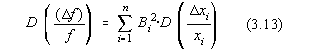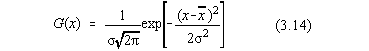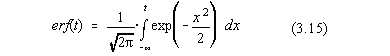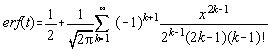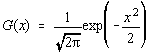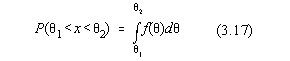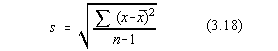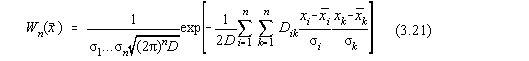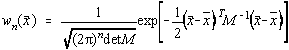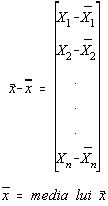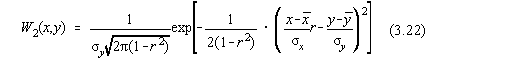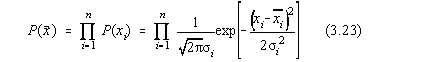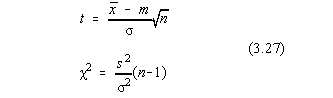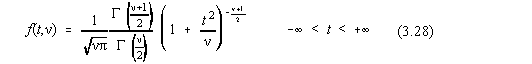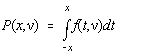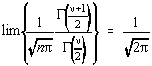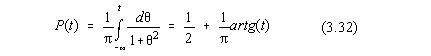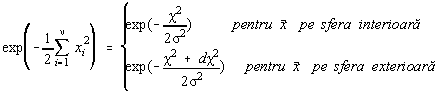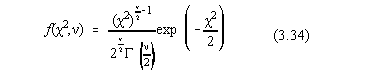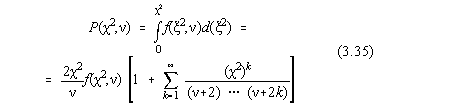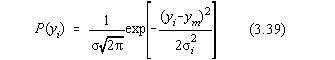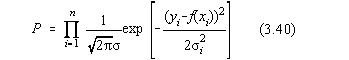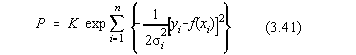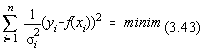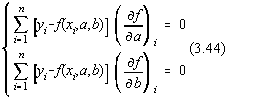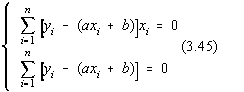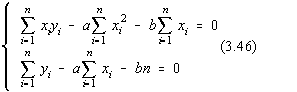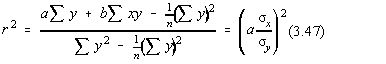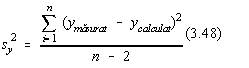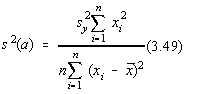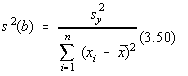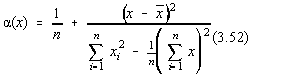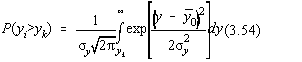3. PRELUCRAREA MASURATORILOR REPETATE
3.1. VARIABILE ALEATOARE SI ERORI EXPERIMENTALE
3.1.1. Notiuni introductive
Valoarea stiintifica a masuratorilor experimentale poate fi evaluata în functie de
[9]:
 modul de obtinere a rezultatelor si
modelele teoretice care le descriu;
modul de obtinere a rezultatelor si
modelele teoretice care le descriu;
 corespondenta dintre numarul
ecuatiilor si cel al necunoscutelor;
corespondenta dintre numarul
ecuatiilor si cel al necunoscutelor;
 nivelul de încredere acordat
rezultatelor obtinute din masuratori;
nivelul de încredere acordat
rezultatelor obtinute din masuratori;
 modul de executie, natura si
raportul dintre marimile masurate.
modul de executie, natura si
raportul dintre marimile masurate.

Fig. 3.1. Clasificarea erorilor experimentale
Deoarece masuratorile experimentale sunt inerent afectate de anumite erori, o
prelucrare corecta a rezultatelor presupune luarea în considerare si caracterizarea
erorilor respective.
Erorile care pot afecta rezultatele experimentale sunt de mai multe feluri (Fig.3.1.):
grosolane, sistematice si întâmplatoare. Pentru caracterizarea erorilor experimentale
pot fi luate în considerare doar erorile întâmplatoare (aleatoare).
Erorile sistematice distorsioneaza rezultatul determinarilor într-un singur sens cu o
dependenta constanta fata de valoarea adevarata. Daca aceste erori sunt constante în
timp, exista speranta corectarii lor prin curbe de calibrare sau alte procedee
stiintifice.
Erorile grosolane (inacceptabile), constituie, de fapt, greseli în experiment si se
pot datora: erorilor personale, deficientelor metodice, erorilor instrumentale sau altor
factori exteriori.
Revenind la erorile întâmplatoare care afecteaza o masuratoare repetata, sa
consideram exemplul tipic al valorii fondului cosmic în cazul unor masuratori de
radioactivitate si exemplul urmator.
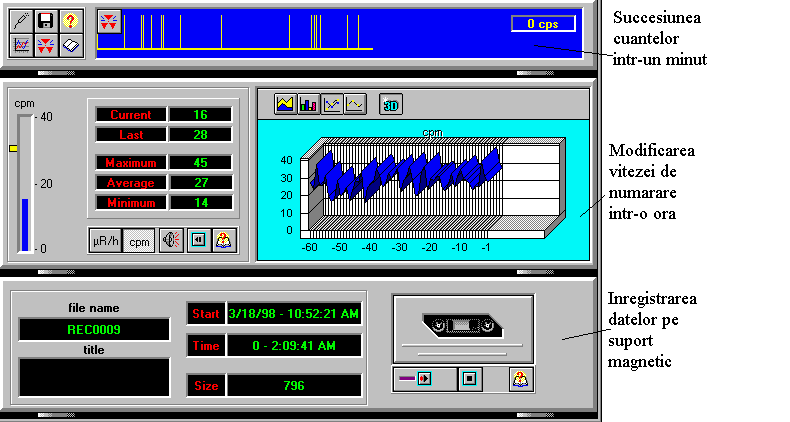
Exemplu:

Alternativ, masuratoarea poate fi efectuata simplu cu un numarator de radiatii gama de
tip "NUMECINT" care afiseaza numarul de cuante gama (impulsuri) numarate
într-un interval de timp prestabilit. Sa presupunem ca afisajul este urmarit si
înregistrat timp îndelungat, de exemplu 3 ore (Fig. 3.2.). Se observa ca numarul de
impulsuri înregistrate variaza între 1 si 21 si se poate întocmi un tabel de forma
celui din Fig.3.2.
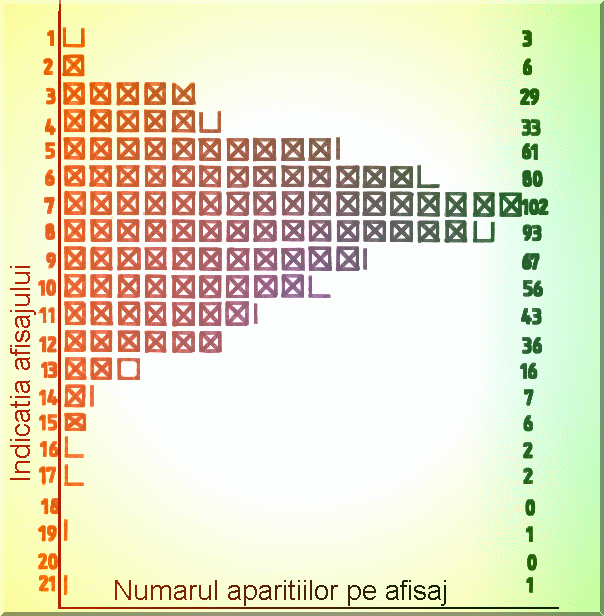
Fig. 3.2. Rezultatul masuratorilor repetate pentru fondul cosmic al radiatiei g .
Marimea 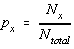 se numeste frecventa de
aparitie a valorii x .
se numeste frecventa de
aparitie a valorii x .
Din acest experiment se observa cu usurinta ca marimea fizica de interes,
"fondul cosmic al radiatiilor gama", variaza aleator între 1 si 21, astfel
încât aceasta marime poate fi tratata în termenii teoriei probabilitatilor. Din tabelul
datelor experimentale identificam "marimile care au sens matematic", de variabila
aleatoare, 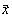 si densitate
de probabilitate
si densitate
de probabilitate 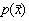 (densitate
de repartitie sau distributia variabilei aleatoare).
(densitate
de repartitie sau distributia variabilei aleatoare).
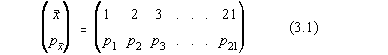
Este evident ca în cazul de fata, fondul cosmic este o variabila aleatoare discreta,
deoarece sunt lipsite de sens fractiunile de cuante gama. Teoretic însa pot fi definite
si variabile aleatoare continue, al caror domeniu de variatie este prin definitie
(-„ ,+„ ).
Numim distributie uniforma, distributia de
probabilitate cu densitate de repartitie constanta.
Pentru o variabila aleatoare continua numim mod orice maxim al densitatii de
repartitie. Astfel, densitatile de repartitie pot fi unimodale sau multimodale. Un minim
al densitatii de repartitie se numeste antimod.
Probabilitatea ca variabila aleatoare x sa ia valori mai mici decât o valoare de
referinta 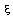 se numeste functie
de repartitie (lege de repartitie) si se obtine ca o suma în
cazul variabilelor aleatoare discrete sau ca o integrala pentru variabilele aleatoare
continue, de la limita inferioara la a densitatilor de probabilitate. Este deci evident ca
aceasta functie este nedescrescatoare. Pe de alta parte, ea este normata la unitate, acest
lucru rezultând din modul de definire al frecventei de aparitie.
se numeste functie
de repartitie (lege de repartitie) si se obtine ca o suma în
cazul variabilelor aleatoare discrete sau ca o integrala pentru variabilele aleatoare
continue, de la limita inferioara la a densitatilor de probabilitate. Este deci evident ca
aceasta functie este nedescrescatoare. Pe de alta parte, ea este normata la unitate, acest
lucru rezultând din modul de definire al frecventei de aparitie.

MEDIA, sau centrul de grupare al evenimentelor, care în cazul nostru este
data de:
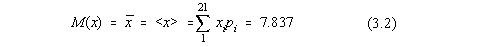
si care ne da valoarea cea mai probabila pentru fondul cosmic.
Media este deci centrul de greutate al densitatii de repartitie si nu media aritmetica
a aparitiilor pe afisaj [10,5]. Pentru variabile aleatoare continue, cu densitatea de
probabilitate P(x), media se defineste ca:
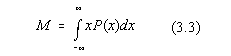

DISPERSIA, utilizata pentru caracterizarea abaterilor valorilor variabilei aleatoare
fata de medie. Pentru variabile aleatoare continue:
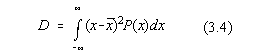
iar pentru variabilele aleatoare discrete:
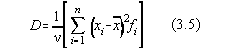
unde neste numarul gradelor de libertate
ale variabilei x,=n-k , k
reprezentând legaturile variabilei aleatoare, în cazul cel mai simplu având valoarea
k=1, adica legatura între variabile este data de media deja calculata, 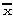 . In cazul acesta, dispersia este:
. In cazul acesta, dispersia este:
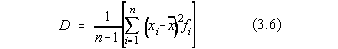
Eroarea patratica medie va fi notata cu s pentru variabilele aleatoare discrete
si cu s spentru variabilele aleatoare continue, 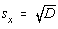 respectiv
respectiv 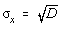 .
.

Daca rezultatele experimentale sunt caracterizate de doua variabile aleatoare, atunci
între acestea se poate defini coeficientul de corelatie:
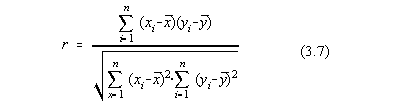
care are valoarea 1 pentru doua variabile dependente si 0 pentru doua variabile
aleatoare independente.
Trebuie remarcat aici ca independenta a doua variabile aleatoare înseamna
ortogonalitate în sensul vectorial si nu "liniar independenta".
Coeficientul de corelatie nu are sens pentru variabile care nu sunt aleatoare.
Observam ca sumele din definitia coeficientului de corelatie pot fi aduse si la forme
mai accesibile:
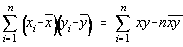
respectiv:
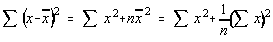
unde n este numarul de esantionari.
Evident, coeficientul de corelatie poate fi definit si pentru variabile aleatoare
continue.
Pentru cazul în care dispunem de n variabile aleatoare, reprezentate prin vectorul 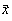 si un alt vector de variabile
aleatoare
si un alt vector de variabile
aleatoare 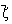 de dimensiune r<n
care îl conditioneaza pe
de dimensiune r<n
care îl conditioneaza pe 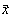 spunem
ca avem o regresie a variabilelor aleatoare
spunem
ca avem o regresie a variabilelor aleatoare 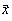 asupra variabilelor aleatoare de tip
asupra variabilelor aleatoare de tip 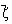 . Prin aceasta definitie se admite implicit ca dimensiunea
vectorului
. Prin aceasta definitie se admite implicit ca dimensiunea
vectorului 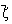 constituie legaturi
asupra vectorului
constituie legaturi
asupra vectorului 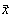 deci numarul
gradelor de libertate va fi n-r.
deci numarul
gradelor de libertate va fi n-r.
3.1.2. Legea propagarii erorilor
Sa consideram acum o functie de repartitie continua multidimensionala a variabilelor
aleatoare 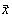 cu mediile
cu mediile 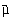 ,
, 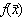 , pe care o dezvoltam în serie în jurul valorilor medii:
, pe care o dezvoltam în serie în jurul valorilor medii:
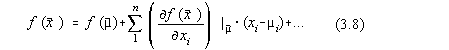
unde n reprezinta numarul variabilelor aleatoare.
Neglijând termenii de ordin superior valoarea medie a functiei 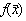 poate fi scrisa ca:
poate fi scrisa ca:
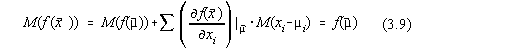
deoarece 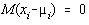 .
.
Dispersia pentru functia 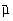 va fi
data de:
va fi
data de:

Deoarece al doilea termen se anuleaza pe domeniul 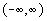 obtinem :
obtinem :
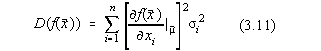
adica legea de propagare a erorilor .
Sa luam exemplul f(x1,x2)=x1x2 cu m1=2;
s 1=0,2 (10%) si m2=3; s 2=0,1 (3.3%). Obtinem:
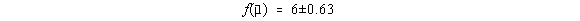
adica o eroare medie patratica de 10.3% .
Variabilele aleatoare xi pot fi neomogene, adica caracterizeza marimi fizice
diferite. In acest caz notam:
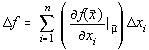
respectiv:
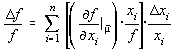
Notând cu:
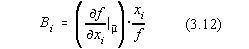
coeficientul de influenta al argumentului xi se obtine pentru
dispersia functiei 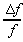 expresia:
expresia:
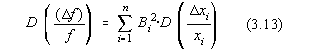
3.2. DISTRIBUTIA NORMALA (GAUSSIANA) SI INTERVALUL DE ÎNCREDERE
Un interes special în caracterizarea erorilor experimentale îl prezinta distributia
normala (Gaussiana) (Fig.3.3.) a carei expresie este data de:
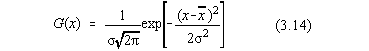
în care 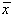 este valoarea
medie, iar se numeste abatere standard. Se poate observa ca din definitia distributiei
Gaussiene are aceeasi semnificatie cu abaterea patratica medie. Aceasta functie a aparut
în teoria molecular-cinetica a gazelor pentru descrierea distributiei vitezelor
moleculelor din gazele ideale.
este valoarea
medie, iar se numeste abatere standard. Se poate observa ca din definitia distributiei
Gaussiene are aceeasi semnificatie cu abaterea patratica medie. Aceasta functie a aparut
în teoria molecular-cinetica a gazelor pentru descrierea distributiei vitezelor
moleculelor din gazele ideale.

Fig. 3.3. Aspectul distributiei normale (Gaussiene).
In cadrul teoriei probabilitatilor densitatea de probabilitate de aceasta forma
se poate obtine pornind de la urmatoarele postulate [9]:
 1. Rezultatele masuratorilor sunt
afectate doar de erori întâmplatoare;
1. Rezultatele masuratorilor sunt
afectate doar de erori întâmplatoare;
 2. Abaterea rezultatului x de la
valoarea adevarata a marimii masurate este cauzata de n factori aleatori, fiecare dintre
acestia producând o eroare elementara;
2. Abaterea rezultatului x de la
valoarea adevarata a marimii masurate este cauzata de n factori aleatori, fiecare dintre
acestia producând o eroare elementara;
 3. Cauzele care provoaca aparitia
erorilor întâmplatoare sunt independente între ele;
3. Cauzele care provoaca aparitia
erorilor întâmplatoare sunt independente între ele;
 4. Probabilitatea de aparitie a
erorilor pozitive este egala cu probabilitatea de aparitie a erorilor negative.
4. Probabilitatea de aparitie a
erorilor pozitive este egala cu probabilitatea de aparitie a erorilor negative.
 5. Erorile foarte mari au aceeasi
probabilitate de aparitie ca erorile foarte mici.
5. Erorile foarte mari au aceeasi
probabilitate de aparitie ca erorile foarte mici.
Prin urmare, repartitia normala a rezultatelor unei masuratori garanteaza absenta
erorilor sistematice.
Functia de repartitie a distributiei normale este notata cu erf(t) (engl. error
function=functie de eroare):
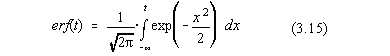
cu substitutia evidenta, 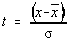 .
.
Prin dezvoltare în serie se obtine:
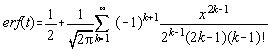
Aceasta functie de repartitie intervine foarte frecvent în problemele de
difuzie, de aceea este foarte eficace calcularea ei cu cinci cifre semnificative folosind
formula lui Hastings [22]:
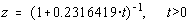
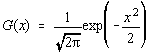
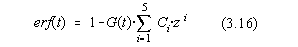
unde:C1=0,31938153; C2=-0,356563782;C3=1,78147937;
C4=-1,821255978;C5=1,330274429.
Propunem urmatoarele cazuri test: erf(0)=0.5, erf(1)=0.84134, erf(2)=0.97725 si
erf(5)=1.
Daca rezultatele masuratorilor sunt distribuite normal, atunci probabilitatea ca x sa
fie cuprins în intervalul (x1,x2) este data de erf(x2)-erf(x1)
( Fig. 3.3).
Pentru a estima corect o marime fizica masurata, în mod obligatoriu trebuie ca acestei
marimi sa-i fie atasta o masura a încrederii în rezultatul obtinut. Pentru o densitate
de probabilitate oarecare f(x), probabilitatea caq 1<x<q 2 este data evident de:
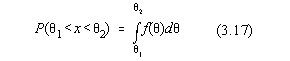
Marimea P se numeste coeficient de încredere si exprima probabilitatea ca
intervalul (q 1, q 2)
sa acopere valoarea adevarata a parametrului q .
Luând ca referinta distributia normala, intervalul de încredere este simetric în
raport cu media si se scrie sub forma
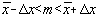
Daca repartitia normala este evaluata în n masuratori, 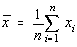 , deci chiar media aritmetica,
abaterea standard de estimatie este data de:
, deci chiar media aritmetica,
abaterea standard de estimatie este data de:
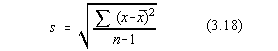
Daca dispunem acum de o valoare adevarata m pe care o comparam cu 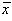 , se poate arata ca variabila z=x este
de asemenea distribuita normal. În acest caz putem efectua substitutia (întâlnita si
anterior):
, se poate arata ca variabila z=x este
de asemenea distribuita normal. În acest caz putem efectua substitutia (întâlnita si
anterior):
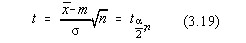
Indicele aare semnificatia a =1-P unde P este
probabilitatea ca 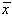 sa acopere
valoarea adevarata m, iar n este numarul gradelor de libertate
ale variabilei aleatoare. Se poate scrie asadar:
sa acopere
valoarea adevarata m, iar n este numarul gradelor de libertate
ale variabilei aleatoare. Se poate scrie asadar:
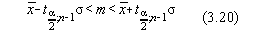
Evident, pentru o distributie normala a rezultatelor masuratorilor, acestea ar
trebui repetate de o infinitate de ori. In practica vom folosi distributii care la limita
tind catre distributia normala si care ne pot garanta absenta erorilor sistematice.
3.3. LEGEA NORMALA MULTIDIMENSIONALA
Legea normala multidimensionala se defineste ca [5]:
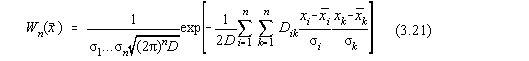
unde D este determinantul:

cu rik=rki, acesti coeficienti fiind coeficientii de
corelatie ai variabilelor aleatoare.
Legea de repartitie depinde de : n parametri s i,
n parametri 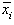 ,
, 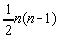 parametri rik, în total
parametri rik, în total 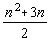 parametri.
parametri.
Legea de distributie mai poate fi scrisa sub forma:
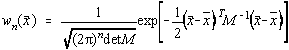
unde elementele matricii M sunt de forma:
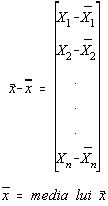
unde Mik=s ikrik, iar
det(M)=s 12 s 22...s n2D.

Fig. 3.4. Modificarea aspectului distributiei normale bidimensionale in functie de
coeficientul de corelatie
În cazul bidimensional legea normala multidimensionala se scrie:
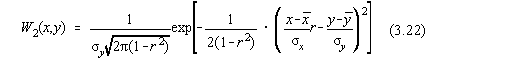
Sa fixam 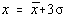 si sa
reprezentam graficele lui
si sa
reprezentam graficele lui 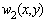 pentru
diferiti coeficienti de corelatie (Fig.3.4).
pentru
diferiti coeficienti de corelatie (Fig.3.4).
Aceasta reprezentare ne arata ca la studiul unui fenomen, spre exemplu în functie de
timp, este obligatoriu ca masuratorile sa fie independente între ele, altfel se produc
erori sistematice.
De asemenea, "îndesirea" arbitrara a punctelor experimentale conduce la
corelatii nenule cu un efect nefast asupra interpretarii. Singura interpolare permisa este
cea liniara, pentru x si y omogene, deoarece astfel nu se modifica r2. Alte
interpolari sunt potrivite doar în absenta erorilor experimentale sau pentru integrari
numerice.
De aceea pentru masuratori independente, folosim formula:
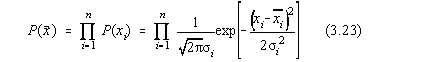
care înseamna ca probabilitatea a n evenimente independente este produsul
probabilitatilor evenimentelor individuale.
3.4. DISTRIBUTIA POISSON
Distributia Poisson are forma:
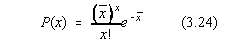
si este normata la unitate. Pentru aceasta distributie este evidenta formula de
recurenta:
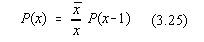
Distributia Poisson este folosita pentru descrierea experimentelor cu un numar
mare de esantionari, de ordinul 103. Ea este foarte potrivita pentru descrierea
fluctuatiilor statistice ale masuratorilor cu contori de radiatii, cum ar fi fondul cosmic
al radiatiei gama.
In cadrul teoriei molecular-cinetice a gazelor, sa aratat ca media patratului
fluctuatiilor numarului de particule dintrun volum mic de gaz, N (fluctuatii mari, în
care 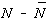 este comparabil cu N) este
data de:
este comparabil cu N) este
data de:
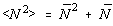
iar dispersia este atunci:
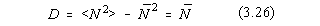
Acest rezultat este deosebit de important deoarece permite o evaluare a
dispersiei în ipoteza unei distributii Poisson a erorilor întâmplatoare pentru
masuratorile cu contori de radiatii. Astfel, daca luam s=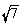 pentru distributia normala asociata masuratorilor fondului cosmic
descris anterior, vom descrie bine rezultatele experimentale (Fig.3.5.).
pentru distributia normala asociata masuratorilor fondului cosmic
descris anterior, vom descrie bine rezultatele experimentale (Fig.3.5.).

Fig. 3.5. Modelarea datelor experimentale din fig. 3.2. cu distributiile Poisson si
Gauss
3.5. TESTAREA ABSENTEI ERORILOR SISTEMATICE
Pentru a dovedi ca întrun experiment nu s-au facut erori sistematice, este necesara
compararea rezultatelor unei masuratori repetate, 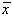 si s, cu un etalon, m,s .
si s, cu un etalon, m,s .
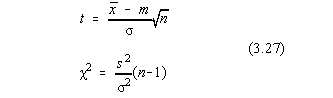
Pe baza proprietatilor distributiei normale ale variabilelor aleatoare, ale
mediei si dispersiei vom testa absenta erorilor sistematice pentru un anumit nivel de
încredere fixat, tipic =0.05, corespunzator unei probabilitati P=90%.
3.5.1. Distributia Student
Aceasta distributie a fost studiata de fizicianul englez Croset (1876-1937) care
folosea pseudonimul Student. Aceasta distributie este unimodala, simetrica si depinde de
doua variabile, t si , unde este numarul gradelor de libertate, deci un numar întreg:
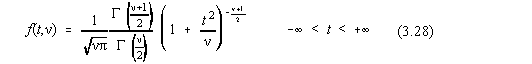
unde G reprezinta functiile hipergeometrice ale lui
Euler iar functia de repartitie este data de:
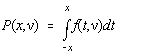
Pentru calculul efectiv al acestei functii [22] facem substitutia 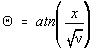 , si presupunem ca x > 0.
, si presupunem ca x > 0.
Distingem doua cazuri:
n
este par si atunci:
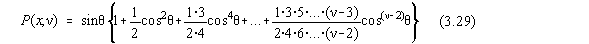
respectiv n impar pentru care:
pentru n =1, 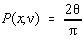
iar pentru n > 1
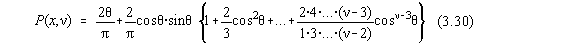
Cazul test propus este: n =10; x=2,13 pentru care
trebuie sa se obtina P=0,9409787 si respectiv n =7; x=3,256
pentru care P=0,98606.
Se poate arata cu usurinta ca pentru distributia Student tinde catre o distributie
normala [9]:
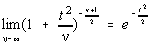
respectiv:
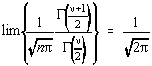
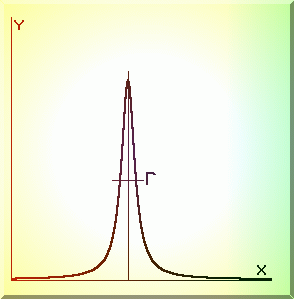
Fig. 3.6. Aspectul distributiei Cauchy (Lorentziene).
Limita inferioara a distributiei Student se obtine pentru n
=1, caz în care obtinem:
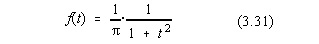
Aceasta este forma analitica a repartitiei Cauchy (forma liniei este o
"Lorentziana", Fig.3.6).
Functia de repartitie a distributiei Cauchy este evident:
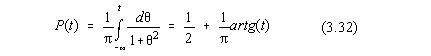
Utilitatea distributiei Student este evidenta prin tipul de înrudire cu
distributia normala. Astfel, dupa repetarea unei masuratori de n ori calculam media
aritmetica 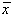 , numarul gradelor de
libertate fiind n=n -1. In ipoteza absentei erorilor
sistematice este posibil ca pentru n masuratorile efectuate sa conduca la valoarea m a
etalonului. Se propune un nivel de încredere si se calculeaza variabila:
, numarul gradelor de
libertate fiind n=n -1. In ipoteza absentei erorilor
sistematice este posibil ca pentru n masuratorile efectuate sa conduca la valoarea m a
etalonului. Se propune un nivel de încredere si se calculeaza variabila:
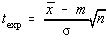
Daca texp < tStudent pentru P=1-a
dat, se admite ca masuratorile efectuate nu au fost afectate de erori sistematice.
Procedeul de testare a absentei erorilor sistematice cu ajutorul functiei de repartitie
Student se numeste "testul t" sau "testul Student".
Pentru folosirea distributiei Student este utila tabelarea functiei P(x,) pentru
diferite probabilitati si grade de libertate.
3.5.2. Distributia
c 2
Aceasta distributie a fost studiata de Helmert si Pearson. Variabila aleatoare luata
în studiu are forma:
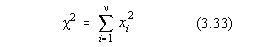
unde xi sunt la rândul lor variabile aleatoare. In acest caz, 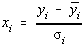 este eroarea elementara la o
masuratoare, iar n reprezinta numarul gradelor de libertate
[9].
este eroarea elementara la o
masuratoare, iar n reprezinta numarul gradelor de libertate
[9].
Considerând doua sfere de raze 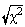 si
si 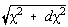 , cautam
probabilitatea ca c n2 < c 2 < c n2+dc 2 pentru un vector aleator (x1,...,xn).
Se observa ca:
, cautam
probabilitatea ca c n2 < c 2 < c n2+dc 2 pentru un vector aleator (x1,...,xn).
Se observa ca:
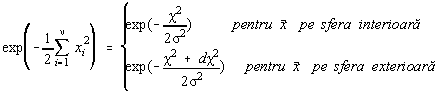
Deoarece c 2 > 0, densitatea de
repartitie a variabilei este nula pentru x < 0. Dupa calculul coeficientilor de normare
la unitate, densitatea de repartitie are forma:
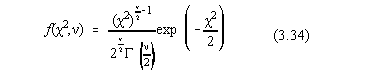
cu proprietatea ca:
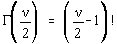 pentru n
par
pentru n
par
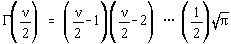
pentru n impar
Functia de repartitie se poate calcula astfel [22]:
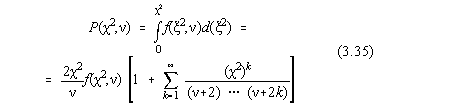
Deoarece calculul sumelor se face cu o precizie finita, data de reprezentarea
interna a numerelor reale în calculator, sumarea se poate încheia atunci când ultimul
termen nu mai modifica valoarea sumei.
Programele exemplificative calculeaza P pentru c 2
si n dat, cazul test propus fiind c 2=8,1;
n =4 cu P=0,912017 respectiv c 2=3,2;
n=7 cu P=0,13410.
Din expunerea facuta rezulta ca dispersia unei variabile aleatoare, c
c2, poate fi evaluata ca:
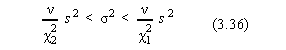
Sa definim variabila:
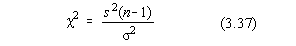
Pentru un interval de încredere , (P=1-a), evaluam 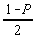 corespunzator conditiei c 2 <c 12.
Din tabelul P(c 2,n) gasim valorile c 12 si c 22
corespunzatoare celor doua limite ale dispersiei. Putem acum sa evaluam intervalul
dispersiei rezultatelor experimentale în domeniul delimitat de c
12 si c 22. Daca
aceste limite încadreaza dispersia etalonului, atunci putem admite absenta erorilor
sistematice în dispersia masuratorilor repetate pentru variabila
corespunzator conditiei c 2 <c 12.
Din tabelul P(c 2,n) gasim valorile c 12 si c 22
corespunzatoare celor doua limite ale dispersiei. Putem acum sa evaluam intervalul
dispersiei rezultatelor experimentale în domeniul delimitat de c
12 si c 22. Daca
aceste limite încadreaza dispersia etalonului, atunci putem admite absenta erorilor
sistematice în dispersia masuratorilor repetate pentru variabila 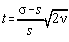 .
.
Acesta este "testul Pearson" sau "testul c 2",
fiind util mai ales pentru un numar mic de esantionari, când asimetria distributiei
rezultatelor experimentale este foarte accentuata. Daca n este
mare, asupra variabilei aleatoare s se poate aplica si testul Student [11].
3.6. SEMNIFICATIA STATISTICA A PRINCIPIULUI CELOR MAI MICI PATRATE
Sa presupunem ca este studiata variatia unei anumite marimi fizice y dupa o variabila
x. Admitem ca marimile y si x sunt legate prin relatia functionala:
y=f(x)
Sa presupunem ca s-au obtinut o serie de puncte experimentale si s-a trasat graficul
lui y în functie de x (Fig.3.7.a).
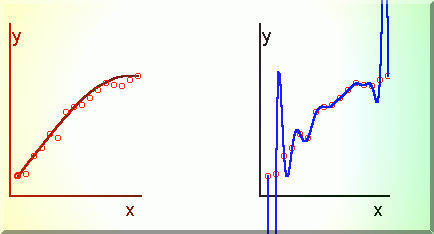
Fig. 3.7. Tendinta generala a unui experiment (a) si rezultatul descrierii prin
interpolare polinomiala de tip Lagrange (b).
In general punctele experimentale nu urmeaza o curba neteda ci prezinta o anumita
dispersie, adica se îndeparteaza aleator de la tendinta generala perceptibila. Aceste
erori experimentale sunt inevitabile, de aceea ne propunem sa gasim o relatie optima
între x si y, care sa evite influenta erorilor experimentale asupra interpretarii
fenomenului studiat. O posibilitate ar fi aceea de a exprima functia f(x) ca un polinom de
grad n-1 (n fiind numarul datelor experimentale). Aceasta idee, perfect fundamentata
matematic, conduce la o curba ondulata care trece exact prin punctele masurate
(Fig.3.7.b), însa desigur nu contine informatii asupra tendintei generale cautate de
comportare a marimii necunoscute. Iata de ce în analiza problemelor de aproximare prin
metoda celor mai mici patrate este important sa propunem noi forma
analitica a functiei f(x), stabilita pe baza unor considerente fizice (teoretice).
Folosind metoda celor mai mici patrate vom cauta parametrii functiei f(x) care aproximeaza
cel mai bine punctele experimentale determinate. De exemplu, pentru o functie de forma:
y=a(b-ecx) (3.38)
vom avea variabila x cunoscuta experimental si trei parametri, a,b,c care trebuie
determinati. O relatie de tipul (3.38), care descrie un experiment se numeste model.
In problemele de tip "cele mai mici patrate", este important ca numarul
determinarilor experimentale (perechi (x,y)) sa fie mult mai mare decât numarul
parametrilor modelului (de exemplu a,b si c din expresia (3.38)), pentru a evita
comportarile aberante despre care am amintit (Fig.3.7.b). Pentru determinarea optima a
parametrilor modelului, va trebui sa tinem cont de existenta inerentelor erori
experimentale.
3.6.1. Metoda celor mai mici patrate
Atunci când apar erori experimentale, este util sa folosim rezultatele teoriei
probabilitatilor. Astfel, daca erorile experimentale sunt întâmplatoare (aleatoare, în
absenta erorilor sistematice sau grosolane) putem presupune ca repetarea unei masuratori
pentru perechea (x,y), adica (x,y1), (x,y2), (x,y3),...
va conduce la o valoare medie (x,ym), valorile ym fiind distribuite
normal în jurul mediei. Distributia normala a valorilor va avea o abatere standard
(Fig.3.3.).
Pentru un x fixat, distributia normala din Fig.3.3. este data de relatia:
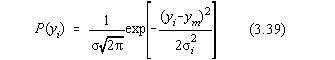
în care ym aproximeaza cel mai bine valoarea medie adevarata, iar P(yi)
reprezinta probabilitatea cu care se obtine valoarea medie adevarata a lui yi.
Daca pentru fiecare x se masoara un singur y, nu se poate determina valoarea ym,
însa este de dorit ca functia model f(x) sa aproximeze pe ym. De aceea în
(3.39) ym va fi înlocuit cu f(x) si presupunem pentru simplitate ca toate
abaterile standard sunt egale:
s
1 = s 2 = ... = s
Vom cauta sa optimizam parametrii functiei f(x) astfel încât aceasta functie sa
aproximeze cât mai bine pe ym în fiecare punct.
Vom calcula probabilitatea ca pentru fiecare masuratoare x, sa obtinem valori în
intervalul ymi+dy. Deoarece masuratorile sunt independente, probabilitatea
totala este produsul probabilitatilor individuale:
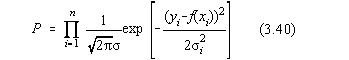
sau:
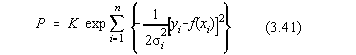

Pentru ca functia model f(x) sa aproximeze cât mai bine datele experimentale,
este necesar ca probabilitatea P sa fie maxima. Din cauza semnului "-" în
exponent, vom avea:
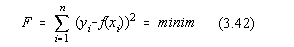
Daca abaterile standard nu sunt egale :
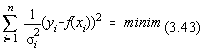
s i2 fiind ponderea statistica a
punctului i.
Aceasta este relatia de baza pentru metoda "celor mai mici patrate",
justificata pe baza ipotezei foarte plauzibile a repartitiei normale a erorilor
experimentale, adica absenta erorilor sistematice [12].
3.6.2.Regresia liniara
Sa presupunem ca functia f(x) depinde de parametrii a si b:
f(x) = f(x,a,b)
Din conditia (3.42) obtinem:
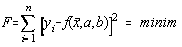
Cei doi parametri a si b pot fi determinati din conditiile ca derivatele partiale
ale functionalei F în raport cu fiecare parametru în parte sa se anuleze. In cazul
general se obtine un sistem cu un numar de ecuatii egal cu numarul parametrilor modelului.
In cazul a doi parametri, sistemul normal asociat experimentului modelat este:
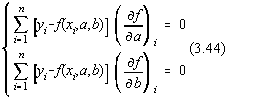
unde 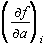 reperezinta
derivata functiei model dupa parametrul a calculata în punctul experimental i. Sistemul
de ecuatii (3.44) are întotdeauna o matrice simetrica.
reperezinta
derivata functiei model dupa parametrul a calculata în punctul experimental i. Sistemul
de ecuatii (3.44) are întotdeauna o matrice simetrica.
Cel mai simplu model polinom este functia de tipul:
f(x) = ax + b
iar determinarea parametrilor a si b prin metoda "celor mai mici patrate" se
numeste regresie liniara.
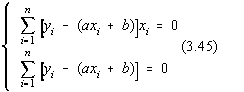
Desfacând parantezele obtinem,
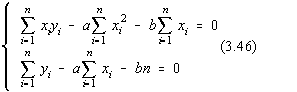
Deci, pentru rezolvarea sistemului va trebui sa calculam sumele care apar în
cele doua ecuatii, apoi sa raportam valorile parametrilor a si b.
Semnificatia coeficientului de corelatie,
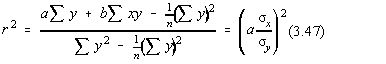
apare evidenta daca ne întoarcem la definitia repartitiei normale bidimensionale
si în exponent se fac înlocuirile y=a+bx si 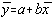 , iar patratul din exponent se ia nul pentru a obtine un minim.
, iar patratul din exponent se ia nul pentru a obtine un minim.
3.6.2.1. Intervalul de încredere la verificarea calibrarii (etalonarii)
Spre deosebire de curba de calibrare care poate fi o curba monotona oarecare, la
verificarea calibrarii ne asteptam ca pentru variabila y sa obtinem aceleasi valori ca
pentru variabila x, adica dreapta de verificare trebuie sa aiba forma: y = a + bx, cu unde
a0 si b1. Pentru aceasta situatie se aplica considerentele de omogenitate din paragraful
3.1.2.
In practica, domeniul de etalonare este foarte frecvent limitat inferior de fond sau de
limita de determinare (Fig. 3.8). Limita superioara a domeniului de etalonare este tipic
conditionata de abaterile de la liniaritate ale dreptei de etalonare.
Insasi definitia regresiei ne permite sa tratam parametrii a si b ca variabile
aleatoare. Numarul gradelor de libertate ale variabilelor aleatoare x si y pentru n
perechi de valori (x,y) este n=n-2.

Fig. 3.8. Dreapta de etalonare, fond si limita de determinare.
În cazul regresiei liniare, notam [11]:
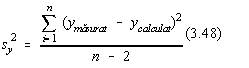
Se poate arata ca si pentru variabilele aleatoare a si b, se pot obtine
dispersiile [10,11]:
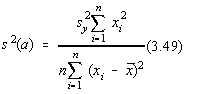
si respectiv:
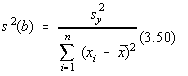
Pentru a demonstra absenta erorilor sistematice în dreapta de etalonare, asupra
variabilelor:
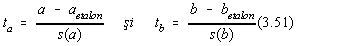
se aplica testul t (Student) pentru un interval de încredere prescris si n-2
grade de libertate.
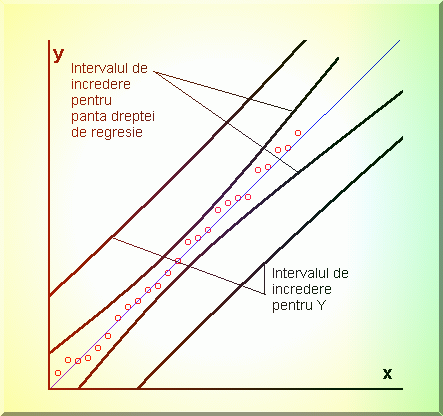
Fig. 3.9. Intervalul de incredere pentru dreapta de etalonare.
Se mai poate arata [10] ca notând cu (x) marimea:
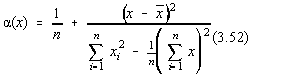
obtinem:
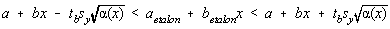
In cazul în care dreapta de etalonare este folosita pentru masuratori efective,
intervalul de încredere pentru marimea evaluata depinde de parametrii etalonarii:
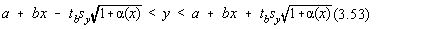
Rezulta ca dreapta de regresie este delimitata sub aspectul intervalului de
încredere de doua arce de hiperbola cu vârful în 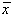 . Intervalul de încredere penalizeaza drastic masuratorile prea
îndepartate de
. Intervalul de încredere penalizeaza drastic masuratorile prea
îndepartate de 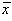 (Fig.3.9.).
(Fig.3.9.).
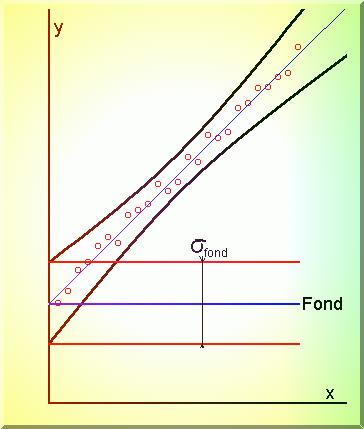
Fig. 3.10. Intervalul de incredere si masuratorile in vecinatatea fondului caracterizat
de o dispersie specifica.
3.6.2.2. Masuratorile în vecinatatea fondului sau a limitei de
determinare
In vecinatatea fondului sau a limitei de determinare, masuratorile bazate pe dreapta de
etalonare trebuie delimitate clar de acesta, tinând cont de intervalul de încredere
pentru dreapta de etalonare si de dispersia fondului (Fig.3.10.).
În ipoteza unei distributii normale a masuratorilor pentru fond, y0 si
pentru xi, yi avem modelul din Fig.3.11.
Presupunând aceeasi abatere standard pentru fond si pentru masuratoarea în
vecinatatea acestuia, probabilitatea ca yi sa fie distinct de y0
este:
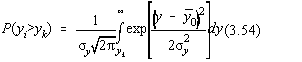
unde introducând variabila 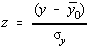 si P(zk)=1 - erf(zk) obtinem valoarea minima care poate
fi raportata:
si P(zk)=1 - erf(zk) obtinem valoarea minima care poate
fi raportata:
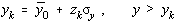
Evident, pentru un numar finit de masuratori,sy poate fi aproximat
folosind distributia c 2.
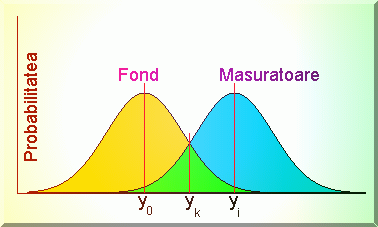
Fig. 3.11. Probabilitatea ca masuratorile în vecinatatea fondului sa fie diferite de
acesta.
3.6.3. Regresia neliniara
Orice functie de forma:
y = a*xb
poate fi adusa la o forma liniara prin logaritmare. Deasemenea, pentru x se pot propune
cele mai diverse forme: x = ln z, x = exp(z), schimbarile de variabila efectuate în
asemenea situatii neafectând formularile deja enuntate.
![]() modul de obtinere a rezultatelor si
modelele teoretice care le descriu;
modul de obtinere a rezultatelor si
modelele teoretice care le descriu; ![]() corespondenta dintre numarul
ecuatiilor si cel al necunoscutelor;
corespondenta dintre numarul
ecuatiilor si cel al necunoscutelor; ![]() nivelul de încredere acordat
rezultatelor obtinute din masuratori;
nivelul de încredere acordat
rezultatelor obtinute din masuratori; ![]() modul de executie, natura si
raportul dintre marimile masurate.
modul de executie, natura si
raportul dintre marimile masurate.